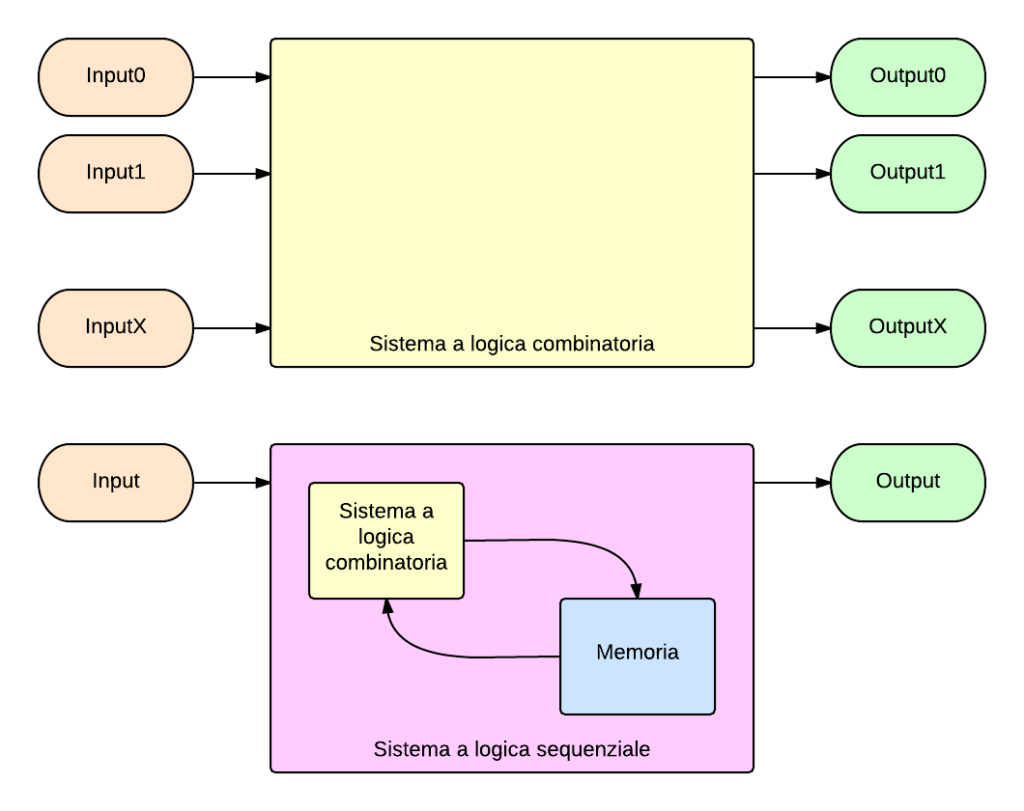
Un sistema digitale può essere visto come una “blackbox”. Questa blackbox riceve degli input (Informazioni in ingresso) e restituisce degli output (informazioni elaborate). La blackbox è la funzione che permette di ottenere dagli input determinati output:
Input e Output possono essere informazioni analogiche o digitali. Le informazioni analogiche vengono “trasformate” in informazioni digitali per essere elaborate. Una volta elaborate, possono essere ritrasformate in analogiche.
I sistemi digitali possono essere:
- sincroni: ogni singola elaborazione rispetta dei tempi prestabiliti da un “clock”. In questa tipologia di sistemi Input e Output possono variare solo allo scattare del clock
- asincroni: l’elaborazione può avvenire in un momento qualsiasi. In questi sistemi Input e Output possono variare in qualsiasi momento
I sistemi digitali possono funzionare con due tipologie di “logiche”:
- logica combinatoria: Per determinati Input in qualsiasi momento otterrò sempre gli stessi Output
- logica sequenziale: Per determinati Input potrei avere degli Output diversi. Questo avviene perché questi sistemi hanno una “memoria” che può influenzare l’Output. L’Output è influenza dallo stato della memoria al momento dell’elaborazione
Specifiche di un sistema digitale
Le specifiche di un sistema digitale sono la descrizione precisa di come un sistema deve funzionare. Le metodologie per definire le specifiche sono le seguenti:
- Utilizzo delle specifiche ad alto livello che definiscono l’insiemi di Input/ Output e la funzione che rappresenta il sistema. Queste informazioni vengono successivamente convertite in binario.
- Utilizzo di una tabella delle verità
- Utilizzo si una macchina a stati finiti
Ad esempio:
Un sistema che dice se un certo mese ha 31 giorni oppure no.
Specifiche ad alto livello:
- Input: x ∈ {1,2,3,4,5,6,7,8,9,10,11,12}. Servono 4 bit per la rappresentazione in binario (x3,x2,x1,x0)
- Output: x ∈ {0,1}. Serve 1 bit per la rappresentazione in binario (z)
- Funzione: z = F(x) = z (x3,x2,x1,x0) = !x3x0 + x3!x0 = x3 XOR x0
- 0 per x = 2,4,6,9,11
- 1 per x = 1,3,5,7,8,10,12
| x | x3 | x2 | x1 | x0 | z |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 1 |
| 11 | 1 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 0 | 0 | 1 |
Per realizzare un sistema digitale si utilizzano semplici componenti:
- Porte Logiche
- Porte Universali
- Memorie Flip-Flop
Porte Logiche e Circuiti combinatori
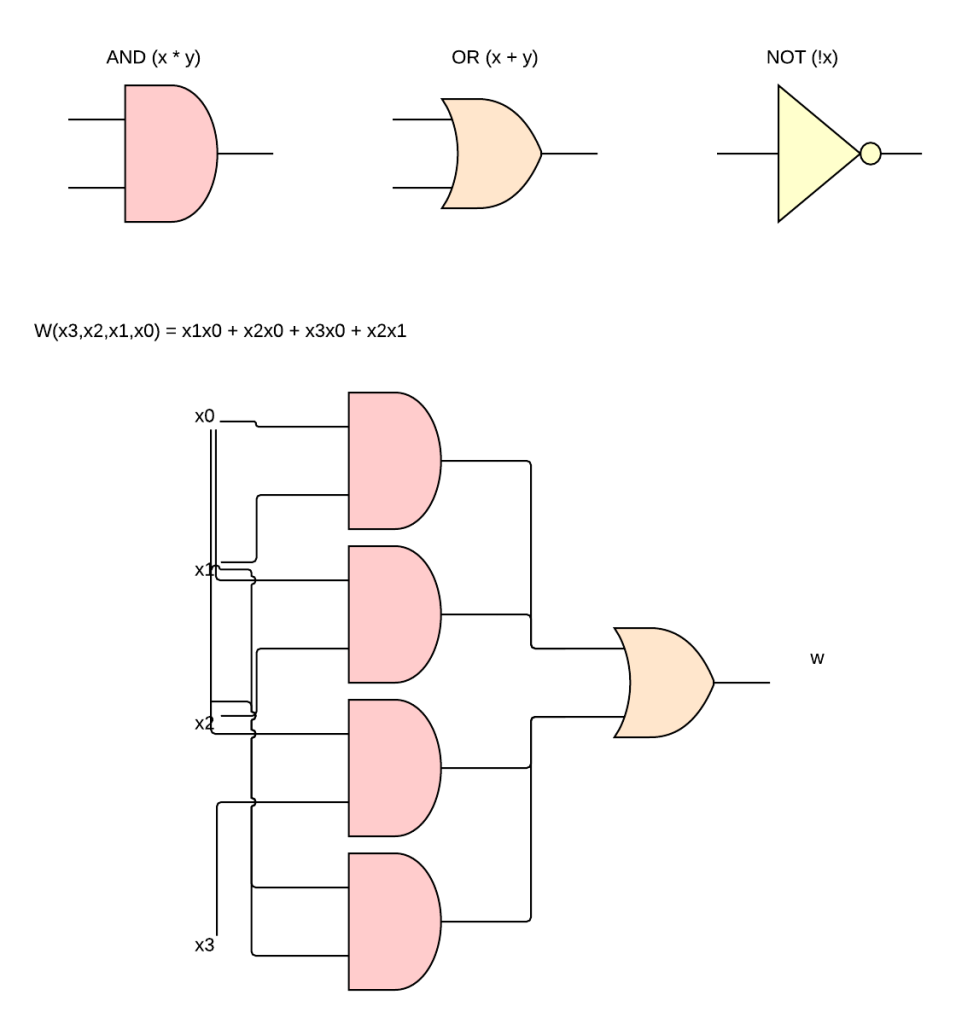
Le porte logiche più semplici sono:
- AND (x * y)
- OR (x + y)
- NOT (!x)
| x | y | AND (x,y) | OR (x,y) | NOT (x) |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
Queste porte logiche implementano le funzioni booleane più utilizzate.
Esempio:
Esistono altre porte logiche:
- NAND (AND negato)
- NOR (OR Negato)
- XOR (OR Esclusivo)
- XNOR (OR Esclusivo Negato)
| x | y | NAND | NOR | XOR | XNOR |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
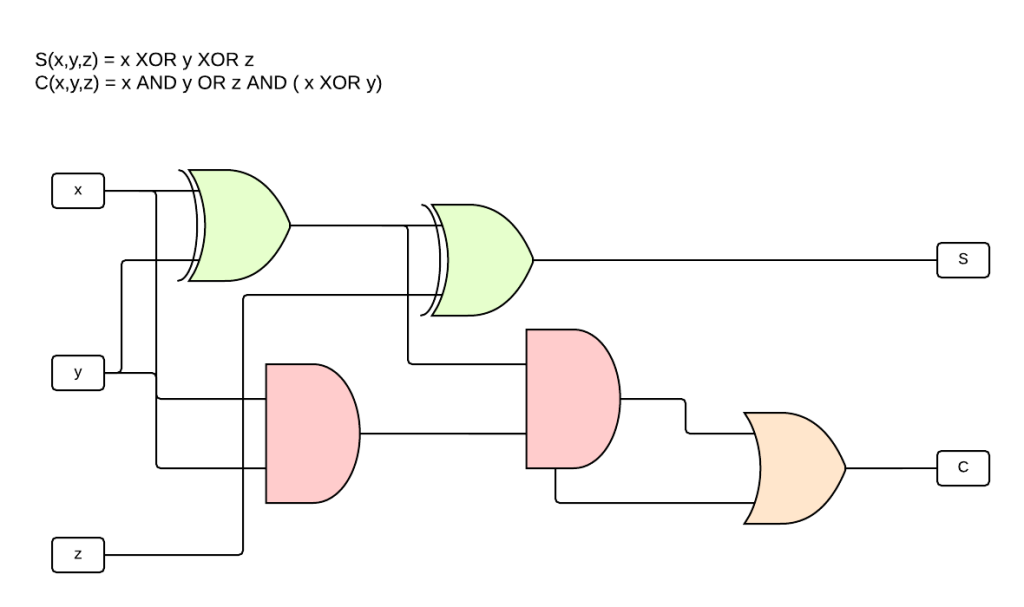
Esempio:
In questo esempio è evidente il “riuso” di alcuni risultati, ad esempio x XOR y viene utilizzata la stessa porta e lo stesso risultato sia per la funzione S che per la funzione C
Porte Universali
Una porta o un insieme di porte è chiamato “Universale” se permette l’implementazione di qualsiasi sistema digitale (Tutte le funzioni Booleane).
Le porte logiche universali standard sono AND, OR e NOT.
Una porta è universale se può implementare le porte universali standard.
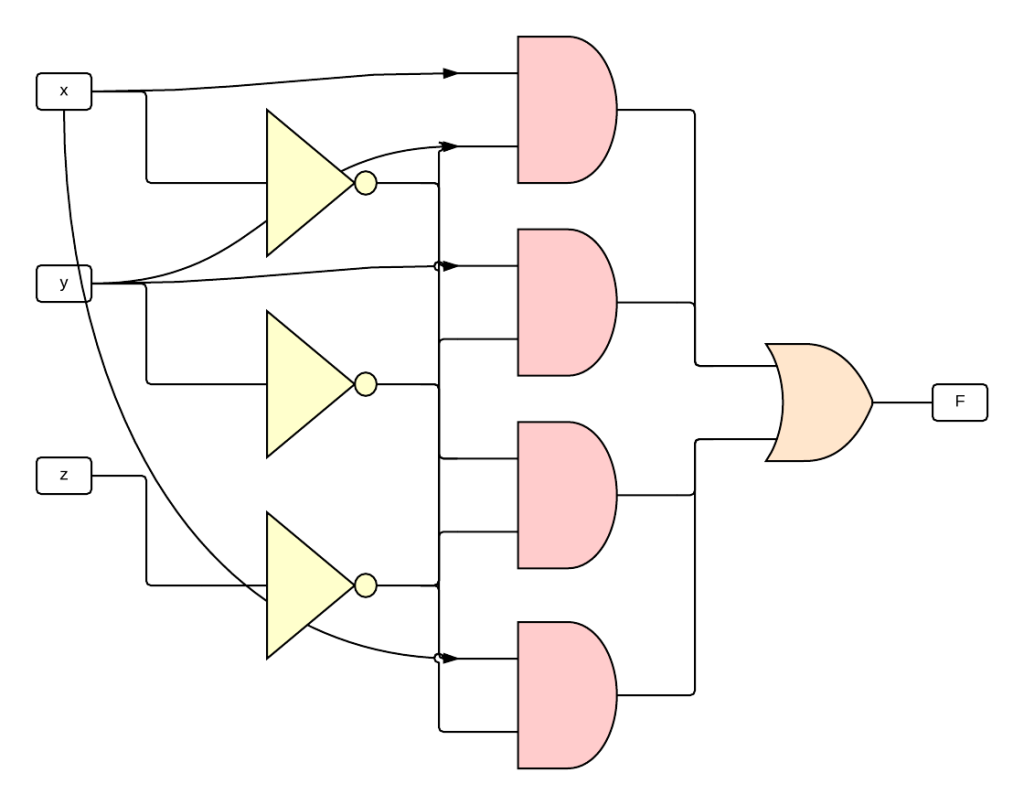
Esempio
f (x,y,z) = !xyz + x!y + !yz
Dimostriamo che è Universale
NOT = f(x,1,1)
!x11 + x!1 + !11 =
!x + x0 + 01 =
!x + 0 + 0 =
!x
Quindi se do come input x, 1 sulla porta y e1 sulla porta z -> ottengo l’inversione di x
OR = f(x,0,y)
!x0y + x!0 + !0y =
0 + x + y =
x + y
Quindi se do come input x sulla porta x, 0 sulla porta y e y sulla porta z -> ottengo x + y
AND = f(x,f(y,1,1),0)
Notare che f(y,1,1) = !y
!x!y0 + xy + y0 =
0 + xy + 0 =
xy
Quindi se do come input x sulla porta x, f(y,1,1) sulla porta y e 0 sulla porta z -> ottengo xy
Per questo motivo posso dire che f è Universale
Semplificazione delle funzioni oppure Ottimizzazione delle funzioni
L’obiettivo della semplificazione delle funzioni è quella di realizzare un sistema digitale con il numero minimo di porte logiche
Esempio
F(x,y,z) = xy!z + !xyz + !x!y!z + x!y!z
Semplificazione:
xy!z + !xy!z + !x!y!z + x!y!z =
!z(xy + !xy) + !y!z(!x+x) =
!z(y(x + !x) + !y!z(1)=
!z(y(1)) + !y!z =
y!z + !y!z =
!z(y + !y) = !z (1) = !z
Tutto il circuito si può implementare con una sola porta NOT!
Per questo motivo il processo di semplificazione è molto importante per ridurre i costi dell’hardware e quindi della manutenzione nell’intero processo di vita di quel sistema. Inoltre il sistema effettuando meno operazioni è più veloce nell’esecuzione delle operazioni.
Combinazioni Don’t care
Esempio
E’ necessario un Encoder che assegna 2 bit ad ogni possibile combinazione di input costituita da 3 bit.
La tabella delle verità è la seguente:
| x | y | z | a | b |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Nella tabella delle verità sono visibili solo 3 combinazioni ma le combinazioni dovrebbero essere 2^3 = 8. Cosa è successo alle altre combinazioni? Questo combinazioni che non vengono prese in considerazioni sono le combinazioni “dont’ care”. Queste combinazioni non sono necessarie per l’implementazione della funzione
Soluzione 1:
a = !xy!z + x!y!z =
z!(!xy + x!y) =
z!(x XOR y)
b = !x!yz + x!y!z =
!y(!xz + x!z) =
!y(x XOR z)
Soluzione 2:
a = !z
b = !y
che usa solo 2 porte NOT
questa soluzione è migliore
Le condizioni don’t care vengono considerate quando:
- alcuni input non verranno mai inviati
- quando alcune parti del circuito non influenzano il risultato della funzione
osservando tutte le condizioni di don’t care è possibile rimuovere delle porte logiche e quindi semplificare il circuito
Circuiti Sequenziali
E’ possibile realizzare una memoria (latch) con due porte NOR:
| S | R | Q | !Q |
| 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 |
La memoria Flip/ Flop è molto più affidabile della memoria Latch ma necessita di 4 porte NAND rispetto alle 2 porte NOR del circuito del latch. Inoltre la memoria Flip/ Flop per funzionare necessita di un clock.
Tabella di eccitazione del Flip/ Flop:
| Q(t) | Q(t+1) | S | R |
| 0 | 0 | 0 | x |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | x | 0 |
Questo significa che se al tempo t il Flip/ Flop si trova nello stato 0 possiamo confermare lo stato 0 inviando su S 0 se invece si trova nello stato 1 possiamo confermare lo stato 1 inviando a R 0. Se invece vogliamo passare da 0 -> 1 dobbiamo settare S=1 e R 0 se vogliamo passare da 1 -> 0 dobbiamo settare S=0 e R=1
Esistono circuiti di memorie Flip/ Flop che usano come input anche un solo segnale.
Esempio
Progettare un circuito con:
- 1 input x
- 3 output A, B, C
Una sorgente esterna invia ad x un bit per ogni ciclo di clock, quando l’input è 0 non avviene alcun cambiamento, altrimenti viene dato come output la sequenza binaria per: 0,1,3,7,6,4.
| Stato Attuale | Stato Successivo X=0 |
Stato Successivo X=1 |
||||||
| A | B | C | A | B | C | A | B | C |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
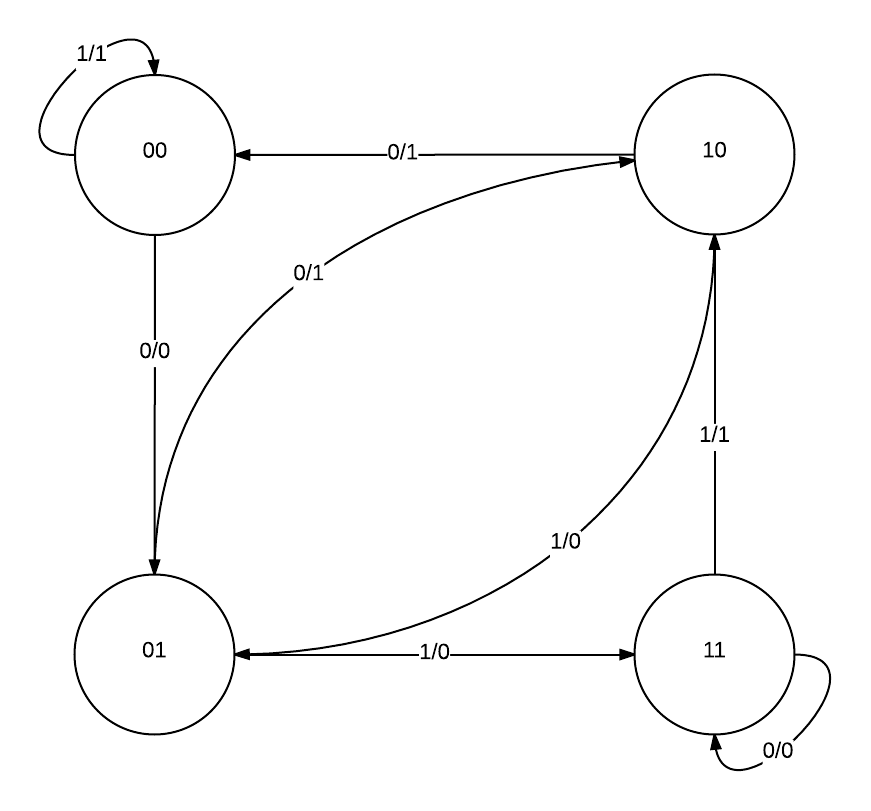
Esempio
Sistema Logico/ Combinatorio
Grafo degli stati e transizioni
Comportamento Flip/ Flop
| Q(t) | Q(t+1) | T |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabella output/ Eccitazione
| Stato Attuale |
Input | Stato Successivo |
Flip/ Flop Inputs |
Output | |||
| A | B | x | A | B | TA | TB | y |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
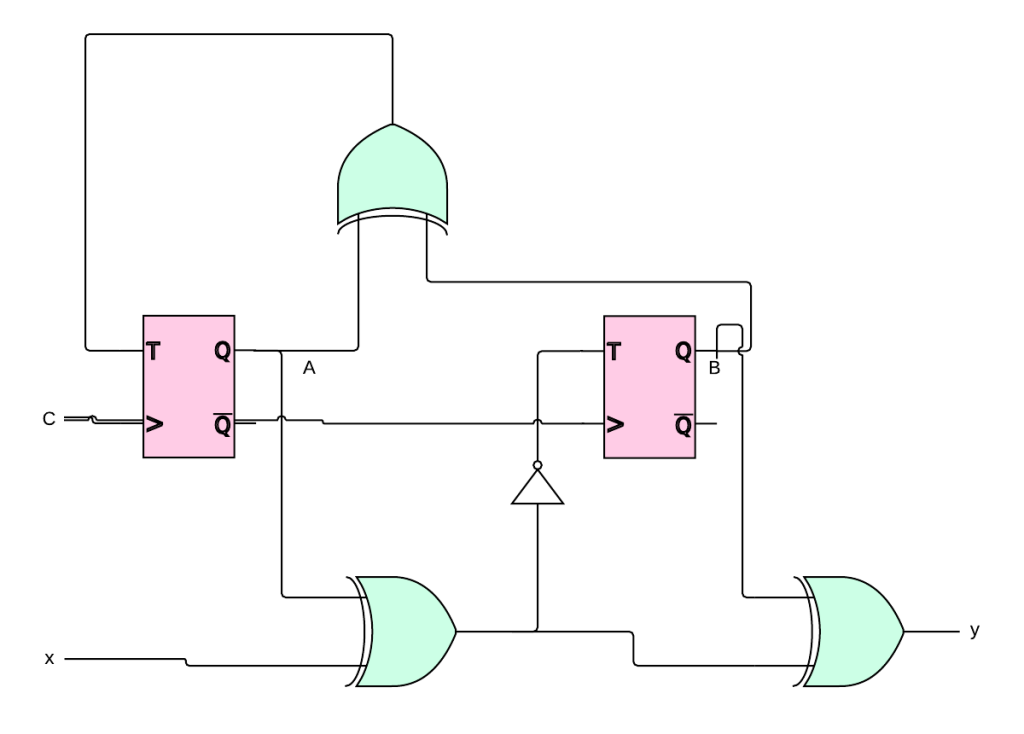
Per realizzare il sistema definiamo le funzioni per i Flip/ Flop e per l’output:
- TA = A XOR B
- TB = !(A XOR B)
- y = A XOR B XOR x
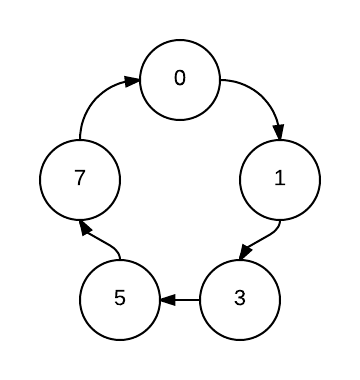
Esempio
Sistema non completamente specificato
Progettare un sistema che genera una sequenza binaria per i seguenti valori 0, 1, 3, 5, 7
| A | B | C | A | B | C | Ta | Tb | Tc | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 5 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 2 | 0 | 1 | 0 | ||||||
| 4 | 1 | 0 | 0 | ||||||
| 6 | 1 | 1 | 0 |
Ta = B
Tb = C
Tc = !C + AB
2,4,6 casi “dont’ care”
